Our household has been playing a lot of the NYT games lately. I find the Letter Boxed puzzle particularly tricky, which gets me thinking, “How could I solve this with a tool?” It’s not too hard to write a function to check if a word follows the rules: subsequent letters must come from different sides of the square. I wondered: could this be solved with a regex?

Let’s start with a simplified version of the puzzle: two sides, and only one letter per side.

A --------- B

What words are allowed here? “A”, “BAB”, “BABA”, “ABA”, and similar.

I originally made a finite state machine diagram to build intuition for creating the regex, but it didn’t seem to help. I’ll try to explain how I’m thinking about the regex choices instead.

1. We might start on the “A” side, choosing that letter. A.
2. Now, we could move to the other side, adding a “B” AB?.
3. In fact, we could bounce back and forth as many times as we want ABAB?, ABABABAB?, ABABABABABAB?. If we try to represent that succinctly, it NDAld be A(BA)*B?.

If we start on the “B” side, the pattern is opposite. Using | to combine our patterns, we get the regex A(BA)*B?|B(AB)*A?. We can annotate it with the purpose of each part of the pattern.

A       start with an "A"
(BA)*   any number of repetitions of "BA" (even zero)
B?      optionally, end with a "B"

|       or

B       start with a "B"
(AB)*   any number of repetitions of "AB" (even zero)
A?      optionally, end with an "A"

More letters on each side

Let’s make the problem a bit harder, adding a second letter to each group:

A         D
  -------
E         M

Now we can spell actual words! “meme”, “dame”, “mama”, “edema”, “made” are all valid. Extending our pattern from the simpler case, we can write

[AE]          Start with A or E
([DM][AE])*   Bounce back and forth any number of times
[DM]?         Optionally, end on the other side.

|

[DM]          Start with D or M
([AE][DM])*   Bounce back and forth any number of times
[AE]?         Optionally, end on the other side.

giving the regex [AE]([DM][AE])*[DM]?|[DM]([AE][DM])*[AE]?.

[AE][AE]
|
[DM][DM]

More sides

What if we make the problem harder in a different way, adding a third side?

A│╲P
 │ ╲
  T

Our words in this case are “pat”, “apt” “tap”, “patata”, “papa”. We can write a regex for this, but it requires a new trick: positive lookahead and lookbehind. Positive lookahead lets a regex “peek” at the next character, without actually consuming it. (For the pedants: it’s possible to rewrite any regex that uses positive lookahead into one that doesn’t. So we don’t need positive lookahead).

(
  A           Start with an A,
  (?=[PT])    make sure it's followed by either a P or a T
 |           or
  P           Start with a P
  (?=[AT])    make sure it's followed by either an A or a T
 |           or
  T           Start with a T
  (?=[PA])    make sure it's followed by either a P or an A
)*            Any number of repetitions of this

[APT]         End with any of A, P, or T

Putting them together

Applying both of these tricks, using groups instead of single letters and positive lookaheads, we can write a regex for a full puzzle.

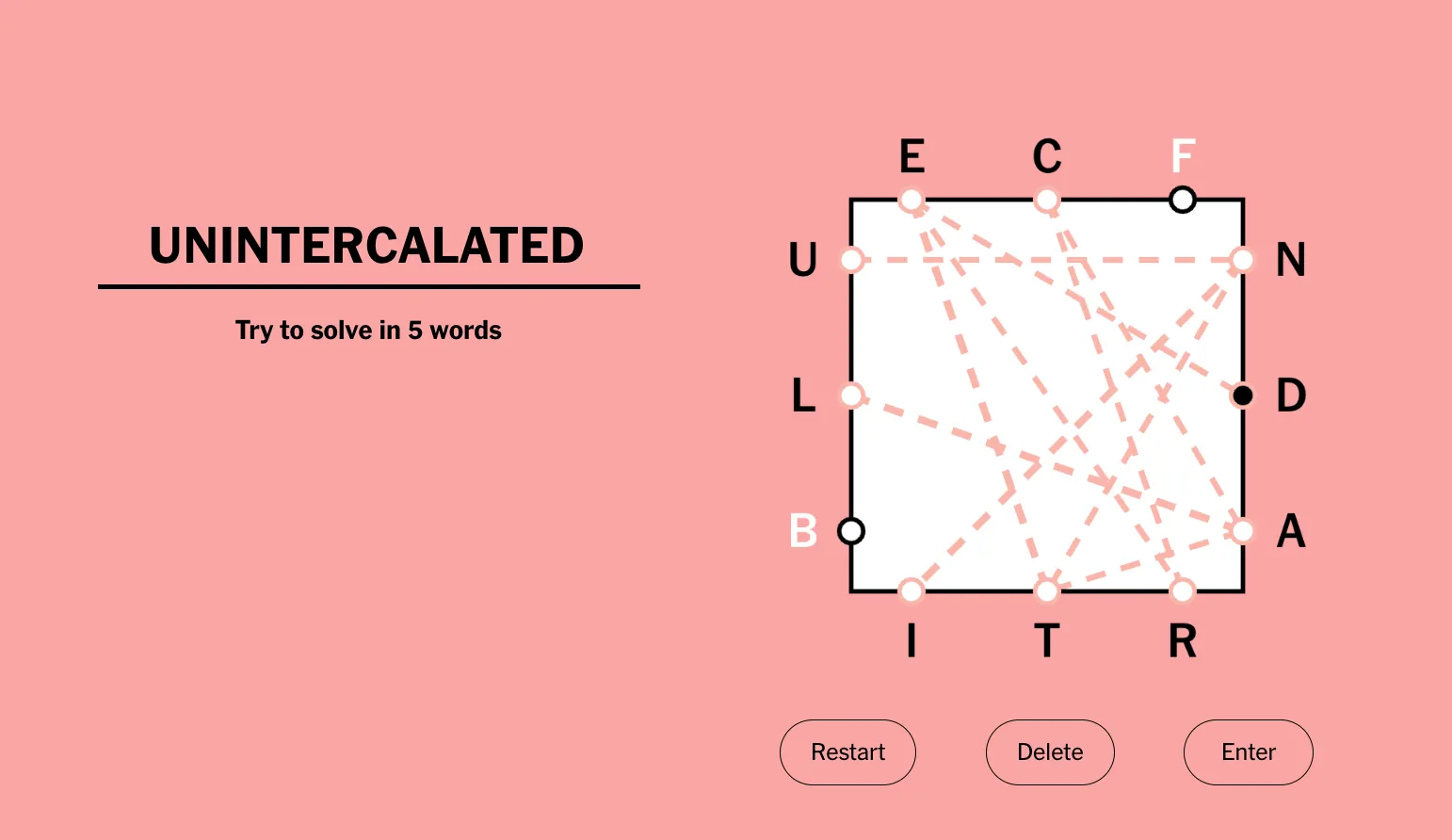
  E  C  F
 ┌────────┐
U│        │N
 │        │
L│        │D
 │        │
B│        │A
 └────────┘
  I  T  R

(
  [ECF]
  (?=[NDAITRULB])
 |
  [NDA]
  (?=[ITRULBECF])
 |
  [ITR]
  (?=[ULBECFNDA])
 |
  [ULB]
  (?=[ECFNDAITR])
)*
[ECFNDAITRULB]

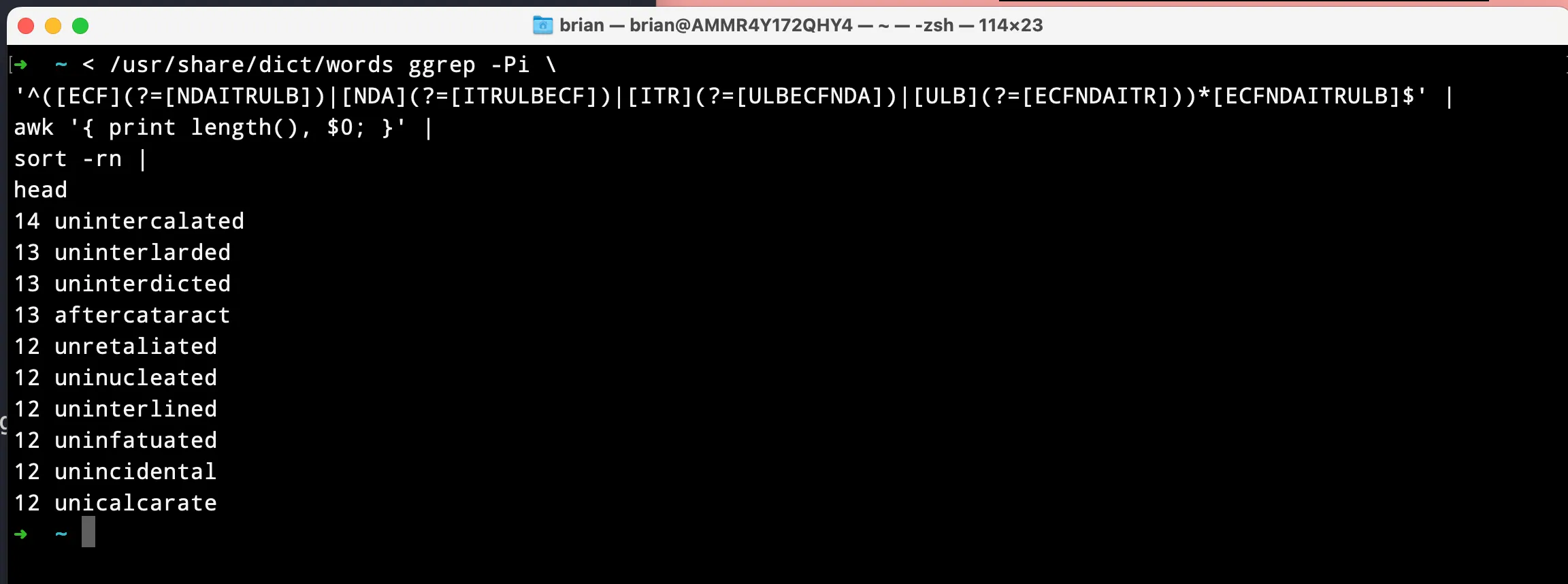
Testing this out requires GNU grep, which has the -P flag to support lookaheads:

< /usr/share/dict/words  # Use the words list as stdin
ggrep -Pi  # I'm on a mac, so GNU grep is named funny.
# our monster regex
'^([ECF](?=[NDAITRULB])|[NDA](?=[ITRULBECF])|[ITR](?=[ULBECFNDA])|[ULB](?=[ECFNDAITR]))*[ECFNDAITRULB]$'
| awk '{ print length(), $0 }' # prefix each word with its length
| sort -rn # put the longest words at the start
| head # only show the top 10